Vector search underpins a wide range of real-world applications—from semantic web search and product recommendations to near-duplicate image detection and anomaly monitoring. In machine learning, for instance, raw text is first embedded as dense vectors through methods such as Word2Vec, GloVe, or transformer-based sentence encoders; this embedding step is a foundational building block used by every modern large-language-model pipeline to retrieve contextually similar words, sentences, or documents.
In that spirit, the synthetic data generation for the Vector Search challenge has been redesigned. We are aligning the challenge with real-world scenarios: rather than following a uniform distribution, the data now forms Gaussian clusters. This introduces meaningful complexity, and demands more sophisticated algorithms for efficient solutions.
Size of the Problem
To guide our decision on the size of the problem, we use the following table of real-world datasets:
| Dataset | Dimension | # Base | # Query |
|---|---|---|---|
| UQ-V | 256 | 1,000,000 | 10,000 |
| Msong | 420 | 992,272 | 200 |
| Audio | 192 | 53,387 | 200 |
| SIFT1M | 128 | 1,000,000 | 10,000 |
| GIST1M | 960 | 1,000,000 | 1,000 |
| Crawl | 300 | 1,989,995 | 10,000 |
| GloVe | 100 | 1,183,514 | 10,000 |
| Enron | 1,369 | 94,987 | 200 |
-
We will keep the dimension fixed at \text{dim}=250, this is a moderate dimension size. This choice is reasonable because techniques such as dimensionality reduction are typically employed to handle larger dimensions; by selecting a moderate dimension size, we eliminate the need for this step.
-
The number of database vectors will scale with the number of queries. We keep the ratio fixed at \frac{\# \text{Database}}{\# \text{Queries}}= 100, this is in-line with real-world data. In particular, we set \#\text{Database}= \lfloor 100 \cdot \#\text{Queries} \rfloor. We keep \# \text{Queries} as the difficulty parameter controlled by the Benchmarkers.
Distribution of the Data
Currently, the data is generated uniformly in the [0,1]^{\text{dim}} hypercube. This is not realistic, as real-world data is typically clustered - benchmarks usually employ Gaussian clusters (see the references [1] and [2]). Therefore, we extend the domain to [-1,1]^{\text{dim}} to allow vector directions to vary. We then sample data using Gaussian clusters.
The Number of Clusters and their Size
To guide our decision on the size of the clusters, we use the following frequently benchmarked datasets :
| Dataset | Domain | # Points | # Classes | Points per Cluster (Ratio) |
|---|---|---|---|---|
| MNIST | Handwritten digits | 70,000 | 10 | 7,000 |
| CIFAR-100 | Tiny images (fine-grained) | 60,000 | 100 | 600 |
| SVHN | House number digits (real-world) | 99,289 | 10 | 9,928 |
| ImageNet-1k | Natural images | 1,281,167 | 1,000 | ~1,281 |
| Tiny ImageNet | Subset of ImageNet | 100,000 | 200 | 500 |
| VGGFace2 | Face recognition | 3,310,000 | 9,131 | ~363 |
| Google Speech Commands v2 | Audio classification | 105,829 | 35 | ~3,023 |
| Wikipedia (small category sets) | Sentences by topic | ~30,000 | 13 | ~2,308 |
The number of clusters will scale with the size of the database, such that \frac{\# \text{Database}}{\# \text{Clusters}}=r_{\text{clust}}=700. This ratio corresponds to medium-grained clustering, which is sufficiently challenging to reflect real-world scenarios. We set the number of clusters to be \#\text{Clusters}= \lfloor(1 + \delta) \cdot \frac{\#\text{Database}}{r_{\text{clust}}} \rfloor for \delta \sim \text{Unif}[-0.05,0.05]. This introduces some noise into the number of clusters.
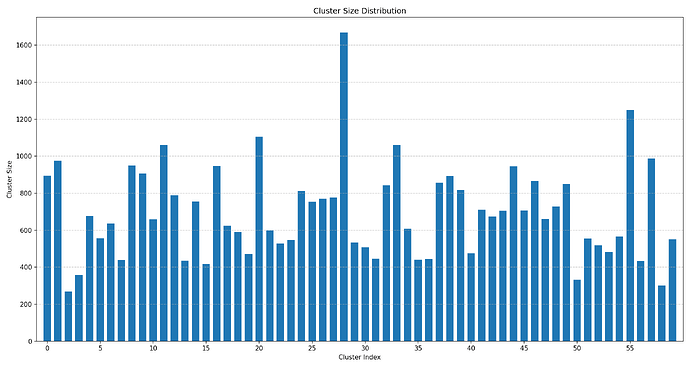
Importantly, clusters will not contain a uniform number of points, as this would be unrealistic. For example, in the MNIST dataset (digits), there is a mild imbalance: digits like “1” and “0” are more frequent than “5” or “9”. In the Wikipedia articles dataset (topic-based), the imbalance is more extreme: common topics like “sports” vastly outnumber niche ones like “theology”. Let K be the number of points in a cluster. For each cluster i, we sample K_i from a log-normal distribution, that is
This distribution is skewed, resulting in many small clusters, some medium-sized clusters, and only a few large clusters. The question becomes how to choose \mu,\sigma^2 : we note that
So that the standard deviation of K is
We pick \sigma^2=0.2, so that the standard deviation scales with the mean as
Setting \mu= \log (r_{\text{clust}})-\frac{\sigma^2}{2}, gives \mathbf{E}[K]=r_{\text{clust}}, as desired. When sampling a database or query point, we sample from cluster i with probability
The following is an example of 60 cluster sizes when sampled in this manner:
The Location and Shape of the Clusters
The cluster vectors will be sampled from truncated multivariate Gaussians \mathcal{N}_{[-1,1]^{\text{dim}}}(\mathbf{\bar{\mu}},\Sigma), such that the samples stay within the region [-1,1]^{\text{dim}}. The mean, \mathbf{\bar{\mu}}, of each cluster will be sampled uniformly from the [-1,1]^{\text{dim}} hypercube. Real-world data is inherently anisotropic, hence we choose
so that the eigenvalues \sigma^2_i vary. Sampling from the truncated multivariate Gaussian is cheap since the components of the Gaussian are independent. To sample x from \mathcal{N}_{[-1,1]^{\text{dim}}}(\mathbf{\bar{\mu}},\Sigma) we sample each component as x_j from \mathcal{N}_{[-1,1]}(\mathbf{\bar{\mu}}_j,\sigma^2_j) directly.
We now choose the variances, \Sigma, so that some discrepancy is kept between the shape of the clusters. We proceed in the following way: for any cluster k\in \{1,\ldots,\#\text{Clusters}\}, we set a mean deviation, \sigma(k), and a range, \epsilon(k), and then sample \sigma_i(k)\sim \text{Unif}[\sigma(k)-\epsilon(k),\sigma(k)+\epsilon(k)].
For each k, \sigma(k) is sampled uniformly in the interval [1,1.1] and \epsilon(k) in the interval [0, 0.05]. This gives a cluster overlap of approximately 8% (that is, 8% of vectors are closer to a cluster mean which is not their own).
Streaming Query Vectors
Currently, all query vectors are received simultaneously, meaning the assignment of nearest neighbours can be optimised globally. However, in many real-world applications - such as real-time recommendation systems or online search - queries arrive sequentially in a stream. This streaming setting introduces new challenges, as decisions must be made incrementally without full knowledge of future queries. We encourage discussion on whether to extended the challenge to incorporate this streaming.
Shimomura, L. C., Oyamada, R. S., Vieira, M. R., & Kaster, D. S. (2021). A survey on graph-based methods for similarity searches in metric spaces. Information Systems, 95, 101507. ↩︎
Wang, M., Xu, X., Yue, Q., & Wang, Y. (2021). A comprehensive survey and experimental comparison of graph-based approximate nearest neighbor search. arXiv preprint, arXiv:2101.12631. ↩︎